When we calculate stresses, we choose a set of orthogonal directions and define the stresses in this co-ordinate system.

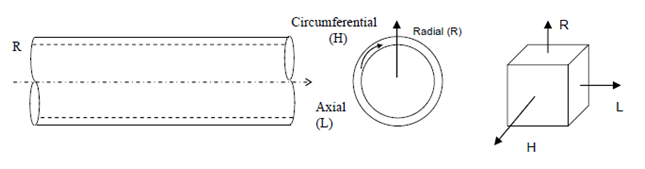
For example, in a pipe subjected to internal pressure or any other load, the most used choice of co-ordinate system is the one comprising of axial or longitudinal direction (L), circumferential (or Hoope’s) direction (H) and radial direction (R) as shown in figure.

Stresses in the pipe wall are expressed as axial (SL), Hoope’s (SH) and radial (SR). These stresses which stretch or compress a grain/crystal are called normal stresses because they are normal to the surface of the crystal.

But, all grains are not oriented as the grain in the figure. In fact the grains would have been oriented in the pipe wall in all possible orientations. The above stresses would also have stress components in direction normal to the faces of such randomly oriented crystal. Each crystal thus does face normal stresses.

[google-square-ad]

One of these orientations must be such that it maximizes one of the normal stresses.The mechanics of solids state that it would also be orientation which minimizes some other normal stress. Normal stresses for such orientation (maximum normal stress orientation) are called principal stresses, and are designated S1 (maximum), S2 and S3 (minimum).

Solid mechanics also states that the sum of the three normal stresses for all orientation is always the same for any given external load. That is :

SL + SH + SR = S1 + S2 + S3

1.  In addition to the normal stresses, a grain can be subjected to shear stresses as well.
2. These act parallel to the crystal surfaces as against perpendicular direction applicable for normal stresses.
3. Shear stresses occur if the pipe is subjected to torsion, bending etc.
4. Just as there is an orientation for which normal stresses are maximum, there is an orientation which maximizes shear stress.
5. The maximum shear stress in a 3-D state of stress can be shown to be :

max = (S1 -S3) / 2

i.e. half of the difference between the maximum and minimum principal stresses.

The maximum shear stress is important to calculate because failure may occur or may be deemed to occur due to shear stress also. A failure perception may stipulate that maximum shear stress should not cross certain threshold value.

It is therefore necessary to take the worst-case scenario for shear stresses also as above and ensure against failure. It is easy to define stresses in the co-ordinate system such as axial-Hoope s-radial (L-H-R) that are defined for a pipe.

The load bearing cross-section is then well defined and stress components are calculated as ratio of load to load bearing cross-section.

Similarly, it is possible to calculate shear stress in a particular plane given the torsional or bending load. What are required for testing failure – safe nature of design are, however, principal stresses and maximum shear stress. These can be calculated from the normal stresses and shear stresses available in any convenient orthogonal co-ordinate system.

In most pipe design cases of interest, the radial component of normal stresses (SR) is negligible as compared to the other two components (SH and SL).

[google-square-ad]

The 3-D state of stress thus can be simplified to 2-D state of stress.

Use of Mohr’s circle then allows to calculate the two principle stresses and maximum shear stress as follows.

S1 = (SL + SH)/2 + [{(SL SH)/2}2 + 2]0.5

S1 = (SL + SH)/2 – [{(SL SH)/2}2 + 2]0.5

= 0.5 [(SL-SH)2 + 4 2]0.5

The third principle stress (minimum i.e. S3) is zero.

All failure theories state that these principle or maximum shear stresses or some combination of them should be within allowable limits for the MoC under consideration.

To check for compliance of the design would then involve relating the applied load to get the net SH, SL, and then calculate S1, S2 and max and some combination of them.

[google-square-ad]