As fluid passes through pipe, it loses its heat to surround atmosphere if its temperature is higher than surrounding air. If temperature of pipe is lower than surrounding air, it gains heat from it. As pipe are generally made from metals like steel, copper etc. which are very good conductor of heat, heat loss will be substantial and very costly. So it is essential to provide cover of a material which is very poor conductor of heat like mineral wool, hemp etc.

[pipingapplinkimage]

Total heat transferred (Q) from pipe through such insulating material depends on following factors  :

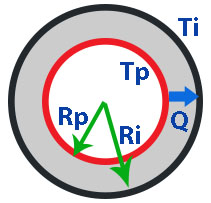
1. N : Length of Pipe.
2. Tp : Operating temperature of fluid inside pipe.
3. Ti : Maximum temperature allowed on the outside surface of insulation. Typically 50°C.
4. Rp : Radius of Pipe.
5. Ri : Radius of Insulation.
6. k : Thermal conductivity of insulating material.

Formula for Steady state heat transfer through insulating material wrapped around a pipe is as follows :

Above equation is derived from Fourier’s equation for heat conduction, for steady state heat transfer for radial heat conduction across hollow cylinder.

Example Calculation

Suppose we have a pipe of  Diameter 12″ with hot oil at a temperature of 200°C flowing through it.  Maximum allowed insulation temperature at the outer wall is 50°C. Allowed heat loss per meter of pipe is 80 W/m. Insulation used is Glass Mineral Wool with thermal conductivity for that temperature range of 0.035W/m.K. Now we have to find out required insulation thickness.

Thermal conductivity is expressed in Watts per meter per Kelvin (W/m.K) which is essentially same as Watts per meter per degree celsius (W/m.C) (There is no multiplier in conversion from Kelvin to degrees. So incremental change in Kelvin is same as incremental change in Celsius.)

In above formula, Q is total heat loss and N is length of pipe. So Q/N becomes our allowed heat loss per meter of pipe which is 80W/m.

Q/N = 80W/m.

Pipe Dia is 12″ hence radius is 6″.

Radius in meters : (6″ X 25.4)/1000 = 0.1524 meters.

So:

80 = 2π × 0.035 × (200-50) ÷ ln(Ri/0.1524)

ln(Ri/0.1524) = 2π × 0.035 × (200-50) / 80 = 0.4123

Hence, Ri = Rp × e^0.4123

Ri = 0.1524 × 1.5103 = 0.2302 m

Hence, insulation thickness = Ri – Rp = 0.2302 – 0.1524 = 0.0777

Insulation thickness = 77.7 mm

Extra margin must be taken on insulation thickness as sometimes conducting heat transfer through insulation may become higher than convective heat transfer due to air on outside wall of insulation. In that case, temperature of outer surface of insulation may increase to more than 50°C.  The purpose of this sample problem is to demonstrate radial heat conduction calculations and practical calculations of insulation thickness also require consideration of convective heat transfer on the outside of insulation wall.